Il est communément admis dans le monde de la finance qu’un risque faible se traduit par un rendement potentiel limité. Réciproquement, un investisseur souhaitant améliorer le rendement de son portefeuille devra accepter de prendre davantage de risques. Ce postulat rejoint l’adage populaire selon lequel « there is no free lunch ». On le retrouve sous plusieurs déclinaisons dans la théorie moderne du portefeuille introduite par H. Markowitz ainsi que dans le Modèle d’Évaluation des Actifs Financiers (MEDAF[1]) développé dans les années 1960, qui permet de déterminer le taux de rendement attendu d’un actif en fonction de son niveau de risque.
Les recherches et les observations empiriques faites sur les marchés financiers ont contribué à l’émergence d’extensions et de modèles alternatifs au MEDAF. À titre d’exemple, Fama-French ont proposé des modèles en identifiant les différents facteurs influençant le rendement d’un actif… dont la capitalisation boursière constituant un indicateur de taille. Dans la pratique et malgré les critiques adressées au MEDAF, celui-ci reste à ce jour le modèle privilégié par une très grande majorité d’analystes et de praticiens. Ces derniers procèdent toutefois fréquemment à des ajustements en marge du modèle, afin de tenir compte des effets de la taille sur le rendement attendu de l’entreprise ou de l’actif qu’ils cherchent à valoriser.
Rendement exigé versus rendement effectif
Les premières études visant à démontrer l’existence de primes de taille ont porté sur l’analyse des taux de rendement effectifs. Au début des années 1980, W. Banz[2] a ainsi étudié la relation empirique entre le rendement et la valeur de marché des actions ordinaires du New York Stock Exchange et concluait que les petites entreprises avaient, en moyenne, des rendements ajustés au risque plus élevés que les entreprises de plus grande taille. Il prenait toutefois la précaution de souligner que ce constat pouvait résulter d’un effet taille ou de plusieurs facteurs inconnus, corrélés à la taille.
D’autres études similaires sont venues corroborer l’existence d’une prime pour les entreprises de petite taille. Les différentiels de rendement observés ex post varient toutefois de manière significative selon les études, en fonction notamment des périodes et des marchés examinés, une prime de taille n’étant d’ailleurs pas systématiquement observée (Crain, 2011[3]).
L’absence de prime observable a posteriori n’est toutefois pas incompatible avec l’hypothèse selon laquelle les investisseurs exigeraient ex ante un rendement plus élevé pour les entreprises de petite taille, leur permettant de compenser les risques additionnels supportés.
Les risques induits par la taille doivent-ils être rémunérés ?
La remise en cause de la prime de taille est souvent opérée à partir de l’argument selon lequel les principaux risques induits par la taille seraient « diversifiables ». La théorie financière distingue en effet (i) les risques spécifiques, dont les effets peuvent être neutralisés grâce à la diversification du portefeuille d’investissements, et (ii) les risques dits systématiques, affectant l’ensemble du marché et ne pouvant être atténués par les stratégies de diversification. Seuls les risques faisant partie de la seconde catégorie sont en principe susceptibles de faire l’objet d’une rémunération.
Parmi les facteurs de risques fréquemment associés à la taille, figurent l’exposition à l’environnement concurrentiel et réglementaire, une dépendance accrue à certaines parties prenantes, un accès restreint aux sources de financement, une concentration du management, une communication financière limitée et une moindre liquidité des instruments financiers échangés (SFEV, 2018[4]). Si certains de ces facteurs sont spécifiques aux entreprises concernées, d’autres recouvrent au moins partiellement des risques de nature systématique. Par ailleurs, la liquidité des titres peut, à elle seule, avoir une incidence significative sur les rendements observés.
Au-delà des arguments théoriques avancés par les opposants et les partisans de la prime de taille, nous soulignons qu’il est difficile dans la réalité de quantifier et d’isoler les parts systématique et spécifique des risques. Il n’est d’ailleurs pas rare que l’annonce d’une entreprise ait des répercussions sur l’ensemble de son secteur, voire du marché. Enfin, il est possible que la perception de certains risques, en principe diversifiables, conduise dans les faits les investisseurs à exiger un surplus de rendement[5].
Le beta des actions traduit-il les facteurs de risque liés à la taille ?
La prise en compte d’une prime de taille, en marge du modèle utilisé pour estimer le rendement d’un titre, suppose que celui-ci n’intègre pas d’ores et déjà la rémunération des risques associés à la taille. À défaut, l’ajustement serait susceptible de conduire à une surestimation du rendement exigé et à une sous-évaluation de l’actif. Pour mémoire, la formule du MEDAF repose sur le coefficient beta, qui est un indicateur de mesure du risque systématique (i.e. non-diversifiable).
Pour apporter des éléments de réponse, nous avons dans un premier temps estimé les rendements implicites[6] des actions d’un panel composé d’un ensemble de sociétés cotées françaises[7]. Nous avons ensuite déterminé pour chacune de ces sociétés le beta de leur action sur plusieurs périodes de référence[8]. La taille des sociétés a été appréhendée au travers de leur capitalisation boursière[9].
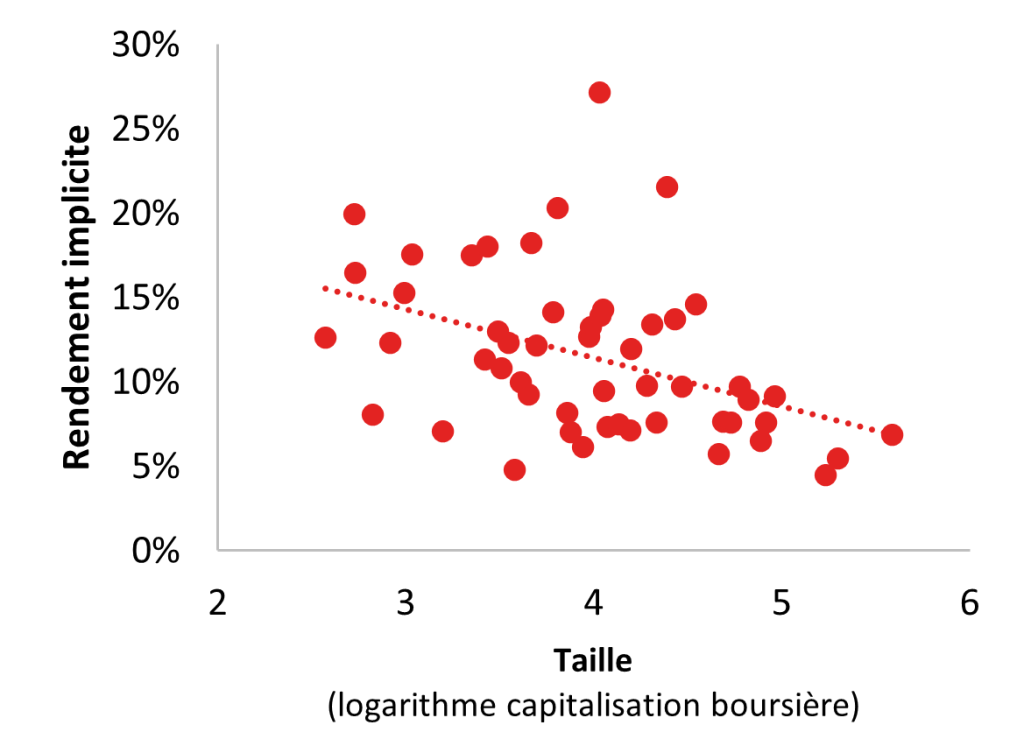
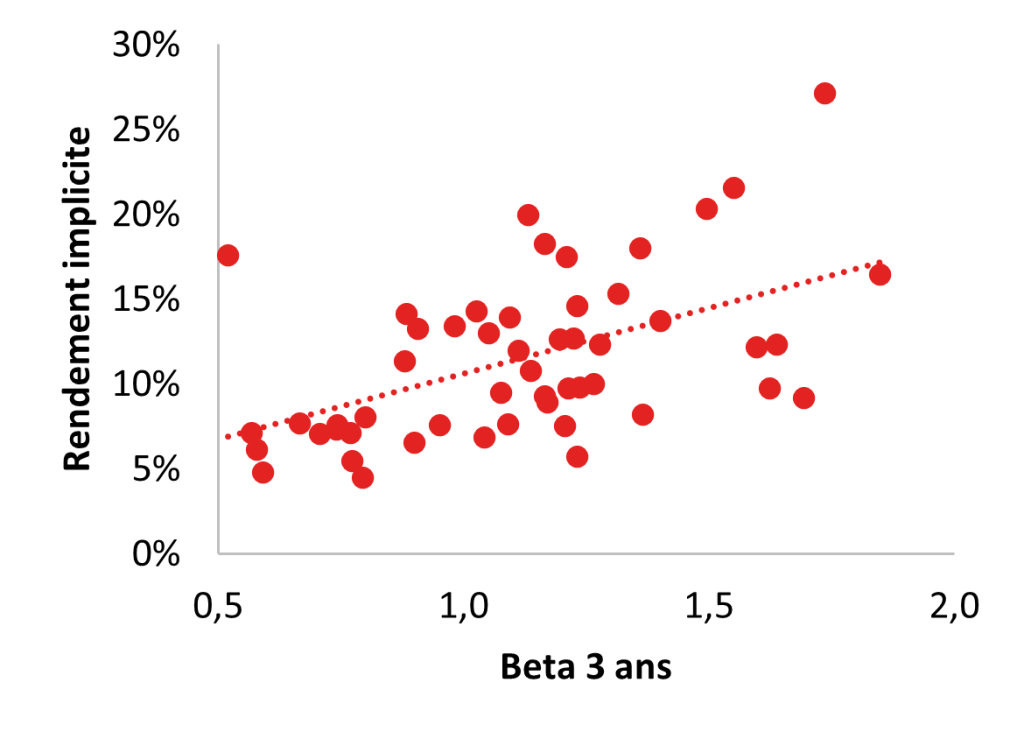
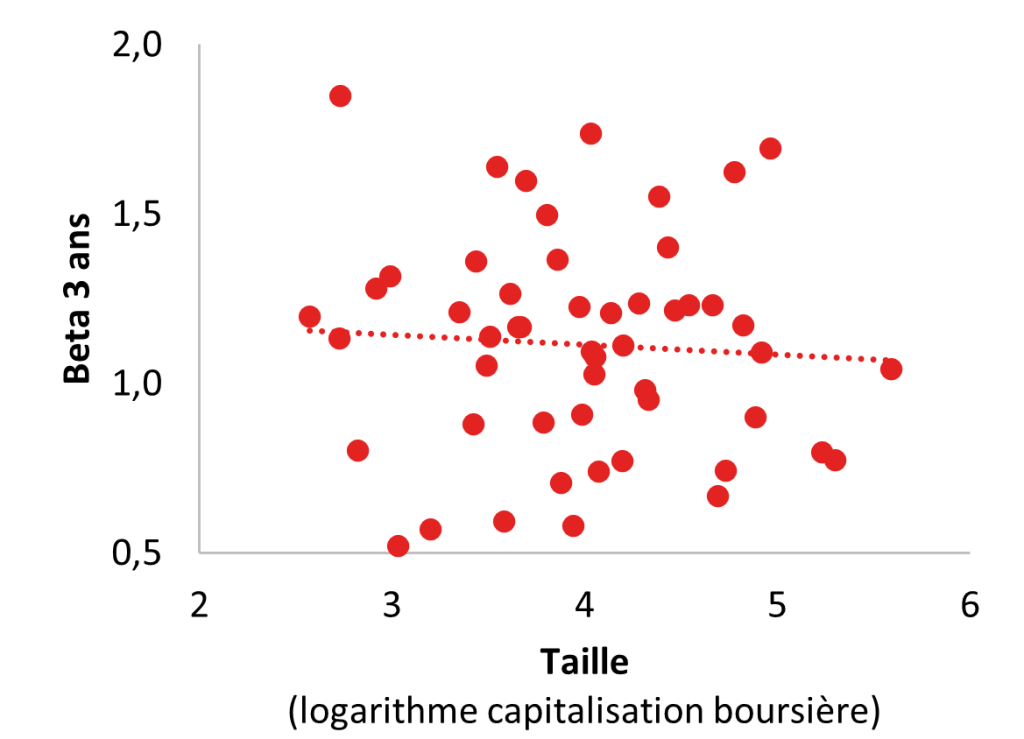
À l’issue de nos analyses, nous observons une corrélation entre, d’une part, les rendements implicites et la taille des sociétés[10] et, d’autre part, entre les rendements implicites et le beta des actions[11]. En revanche, nous n’observons aucune corrélation significative sur le plan statistique entre la taille des sociétés et le beta des actions, quelle que soit la période de référence :
Analyses de régression entre le rendement implicite, la taille et le beta
 |
 |
 |
Source de données : Bloomberg
En outre, nous constatons que la mise en place d’un modèle multifactoriel intégrant à la fois le beta et une variable relative à la taille permet d’estimer le rendement implicite avec une meilleure qualité prédictive. Bien que l’interprétation de ces résultats soit rendue délicate par la multitude des facteurs ayant une incidence sur le beta des actions, il semble ainsi que le coefficient beta ne permette pas de capter correctement les effets de la taille sur le rendement exigé par les investisseurs.
Ce constat peut notamment s’expliquer par le fait que les cours des actions des “small caps” n’incorporent pas immédiatement l’ensemble des informations de marché disponibles, ce phénomène ayant tendance à entraîner une sous-estimation de leur beta. Par ailleurs, une liquidité restreinte est susceptible de conduire les investisseurs à appliquer une décote sur le prix[12], laquelle vient majorer le rendement implicite sans nécessairement modifier le beta de l’action.
Incidence de la taille sur le couple rendement-risque
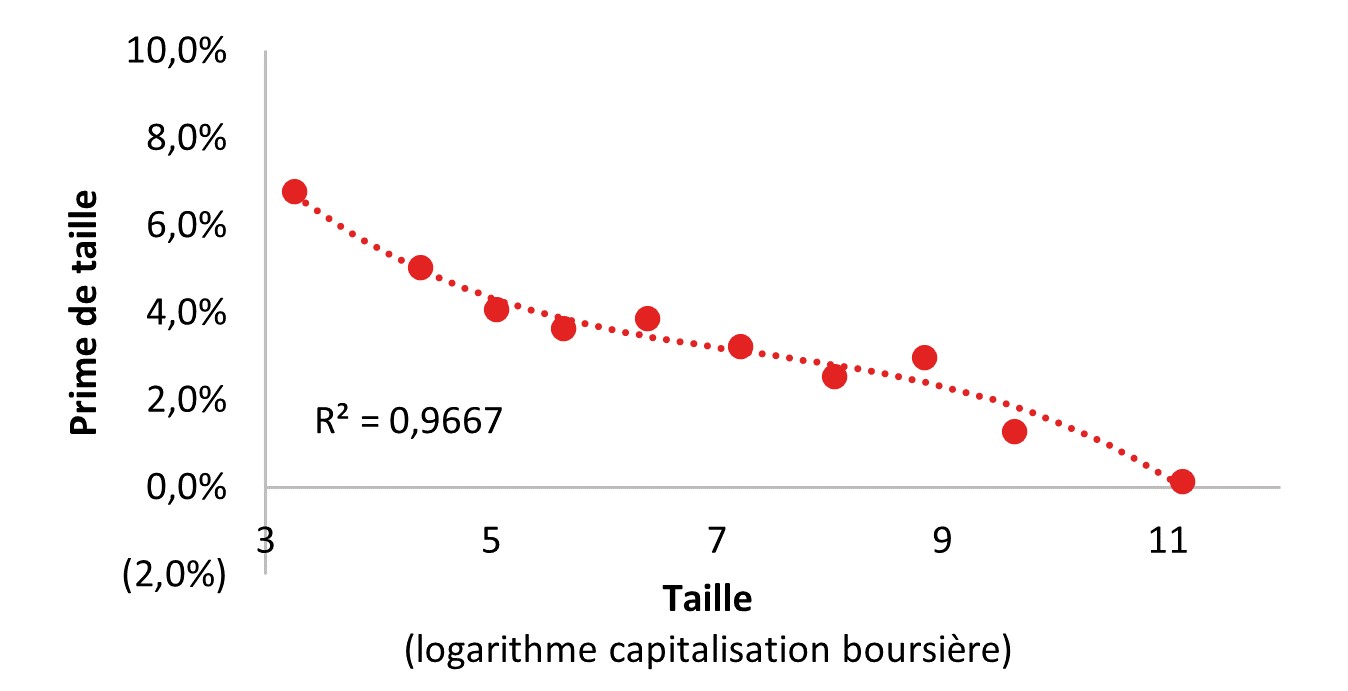
Notre étude portant sur les rendements implicites des actions permet de déterminer, en fonction de la capitalisation boursière[13], le niveau moyen des primes de taille :
Estimation des primes de taille sur le marché français
 |
Source de données : Bloomberg
Les analyses statistiques apportent un éclairage technique, étant toutefois précisé qu’une prime de taille ne peut être automatiquement appliquée sans tenir compte des caractéristiques propres à chaque entreprise. Nous rappelons en outre que :
- la prime de taille doit être calibrée de manière homogène et cohérente avec la prime de marché[14];
- elle varie en fonction de la méthode d’évaluation retenue. Dans le cas d’une approche analogique, si les sociétés à partir desquelles sont déterminés les multiples sont d’une taille comparable, la prime de taille ne trouve généralement pas à s’appliquer[15].
En définitive, l’application d’une prime de taille peut, dans certains cas, s’avérer nécessaire pour aboutir à des résultats pertinents et éviter une prise de décisions fondée sur une mauvaise appréhension du couple rendement-risque. Elle nécessite toutefois des analyses préalables et la mise en œuvre d’un jugement professionnel.
Par Romain Delafont
[1] CAPM (Capital Asset Pricing Model) en anglais.
[2] Banz (1981), The relationship between return and market value of common stocks, Journal of Financial Economics, Volume 9, Issue 1, p. 3-18.
[3] Crain (2011), A literature review of the size effect.
[4] SFEV (2018), Groupe de travail sur les « primes et décotes dans le cadre des évaluations financières ».
[5] Notamment si les investisseurs estiment ne pas être en mesure de contrôler totalement les risques spécifiques par la diversification, contrairement à l’un des postulats du MEDAF.
[6] Les rendements implicites ont été déterminés à partir d’un modèle prospectif, consistant pour chaque société du panel, à calculer le taux qui égalise le cours de bourse et la valeur actuelle des résultats prévisionnels estimés à partir des consensus d’analystes.
[7] Notre étude porte sur les sociétés incluses dans les indices boursiers CAC All Tradable et Euronext Growth All Share.
[8] À la différence des rendements que nous avons estimés de manière prospective, le beta est calculé à partir des données de marché historiques. Le beta étant susceptible de varier de manière significative au cours du temps, nous avons recherché les éventuelles corrélations sur plusieurs périodes de référence.
[9] Sur une échelle logarithmique.
[10] Les rendements implicites sont, en moyenne, plus élevés (faibles) pour les petites (grandes) capitalisations boursières.
[11] Les rendements implicites sont, en moyenne, plus élevés (faibles), pour les titres à beta élevé (faible).
[12] Les facteurs de risques liés à la taille et à la liquidité sont souvent examinés de manière conjointe, les titres des entreprises de plus petite taille présentant généralement, toutes choses égales par ailleurs, une moindre liquidité.
[13] Les capitalisations boursières de notre panel ont été ordonnées en déciles. Nous avons déterminé, pour chaque décile, le rendement moyen implicite des titres le composant. La prime de taille est déterminée par différence entre le rendement moyen du décile et le rendement de marché.
[14] La prime de taille et la prime de marché peuvent ainsi être fondées sur les mêmes données de marché.
[15] Les multiples intègrent en principe d’ores et déjà la perception par le marché des risques associés à la taille.